Teaching experience and interests
My teaching interests are in the broad field of Statistical Physics, condensed-matter physics and biophysics. At the university of Orléans I am currently giving the following courses:


  • Introduction to condensed matter physics
  • Introduction to elasticity theory
  • Selected topics in theoretical biophysics
  • Mathematical methods for the physical sciences



Teaching material

F. Piazza
Selected topics on protein dynamics
Lectures delivered in November 2013 at Tsinghua University, Beijing and in November 2016 at UACM, Mexico city
Notes

F. Piazza
Selected topics in diffusion
Lectures delivered at the University of Florence, ERASMUS Ph.D. course, 2012 and 2013
Notes

F. Piazza
Statistical analysis of DNA sequences
Lecture delivered in July 2002 at: International IP-SOCRATES summer school on nonlinear time series analysis
Power Point slides (might give weird symbols on some platforms)



Selected topics in physical biology, Ph.D. course (Tsinghua University, Beijing, UACM, Mexico city and University of Orléans)

This course is intended to present some recent advances in physical biology, covering mainly two topics, (i) coarse-grained models of protein dynamics and (ii) diffusion- limited bimolecular reactions with an emphasis on di usion in crowded and con ned environments. The course is open to all Ph.D. students in the scientifc doctoral schools. A background in elementary statistical mechanics and calculus is required but no pre- requisite in molecular and cell biology is needed, as a basic introduction to this will be given. The most complex mathematical derivations are done in full length and at slow pace, covering all details in a self-contained manner. The course is structured in about 8 courses of 2 hours, two of which can be organized as exercise classes, with the possibility of both supervised problem solving and running individual or group sessions of computer simulations and calculations, covering aspects treated during the lectures. The material for these (computer codes etc.) are supplied by the instructor. Students have the possibility to set up their personal laptops to use them for the exercise classes.

  • LECTURE 1:

    Introduction to the most important biomolecules in molecular and cell biology. A personal account on the basic building blocks of biological matter.

  • LECTURE 2:

    Statistical physics models of DNA and basic concepts of polymer physics. The case of DNA pulling by optical tweezers.

  • LECTURES 3-4:

    • Modeling protein dynamics I. Force fields and normal mode analysis.
    • Modeling protein dynamics II. Elastic network models, an account on how exceedingly simple modeling schemes still teach a lot on biologically relevant issues.

  • LECTURES 5-8

    • Diffusion-limited bimolecular reactions I. Modeling reactions in the liquid phase through boundary value problems. The classic Smoluchowski and Debye theories.
    • Diffusion-limited bimolecular reactions II. Cells uniformly covered in receptors versus cells with a single, large cluster of receptors. Which is better? A (not so?) surprisingly simple answer from a complex (but instructive) mathematical model.
    • Diffusion-limited bimolecular reactions III. The concept of diffusive interaction. Are two closely spaced receptors as effective as two separated ones, more or less effective?
    • Diffusion-limited bimolecular reactions IV. Towards realistic modeling of transport in the cell. Selected topics in diffusion in crowded environments. What do simple stochastic processes teach us on this subject?



Cours introduction au calcul scientifique, L2 Universite d'Orleans


Cours de langage et calcul scientifique, L3 Universite d'Orleans

  • Lecture 1
  • Lecture 2
  • Lecture 3
  • Lecture 4
  • Lecture 5
  • Lecture 1
  • Lecture 7
  • Lecture 8
  • FORTRAN 90 code for molecular dynamics simulations.
  • FORTRAN 90 code for discrete Fourier transform.
  • FORTRAN 90 code to integrate Gompertz's model (simple Euler O(1)).
  • FORTRAN 90 code to integrate Gompertz's model (simple Euler O(1), modular architecture with subroutines and functions).
  • FORTRAN 90 code to integrate Gompertz's model (modified Euler O(2), predictor-corrector).
  • Sample FORTRAN 90 code to integrate a one-dimensional flow displaying two saddle-point bifurcations (modified Euler O(2))
  • FORTRAN 90 code to integrate a one-dimensional flow using functions and subroutines (modified Euler O(2)). The code also computes the nearest fixed point to the initial condition (steepest descent) and performs a linear stability analysis around this point. The code is meant to illustrate the idea of large-amplitude branches of fixed points.
  • FORTRAN 90 code to integrate a one-dimensional stochastic flow with the Milshtein method. This example illustrates the simple (but non-trivial!) linear stochastic equation with multiplicative noise. This code outputs a file with a single stochastic trajectory labelled by the seed used.
  • FORTRAN 90 code to integrate a one-dimensional stochastic flow with the Milshtein method. This example illustrates the simple (but non-trivial!) linear stochastic equation with multiplicative noise. This code performs averages over a given number of independent stochastic trajectories and outputs the average trajectory and its standard error on the mean.
  • FORTRAN 90 code to integrate a two-dimensional linear dynamical system with the predictor-corrector (modified Euler) method. This code is inspired by the famous paper by Steven Strogatz: Love affairs and differential equations, Math. Magazine, 61, 35 (1988).
  • FORTRAN 90 code to integrate a 2D nonlinear system of the kind {\dot(x1) = F1(x1,x2),\dot(x2) = F2(x1,x2)}. The code uses a 4th order Runge-Kutta algorithm. This example illustrates the case of a non-hyperbolic fixed point, a center which is changed into a spiral by arbitrarily small nonlinear terms (proportional to the parameter a, whose sign controls the stability of the spiral). This example is example 6.3.2 in S. Strogatz's book "Nonlinear dynamics and chaos" The code can be easily generalized to higher dimension and to different nonlinear systems.
  • FORTRAN 77 code to integrate a tabulated function (Simpson)
  • FORTRAN 90 code to compute the relaxation to equilibrium of the money distribution in a system of agents trading pairwise according to microscopic rules preserving the total amount of money in the system. Based on the paper:
  • A. Dragulesku and V. M. Yakovenko
    Statistical mechanics of money
    Eur. Phys. J. B - 17 723-729 (2000)
    PDF file

  • LAPACK subroutine DSYEV + dependencies
  • NORMAL MODE ANALYSIS
    Example: HIV-1 PROTEASE, PDB code: 4HVP
    Elastic network model, alpha-C coarse-graining, sharp cutoff interactions (Rc = 10 Ang)



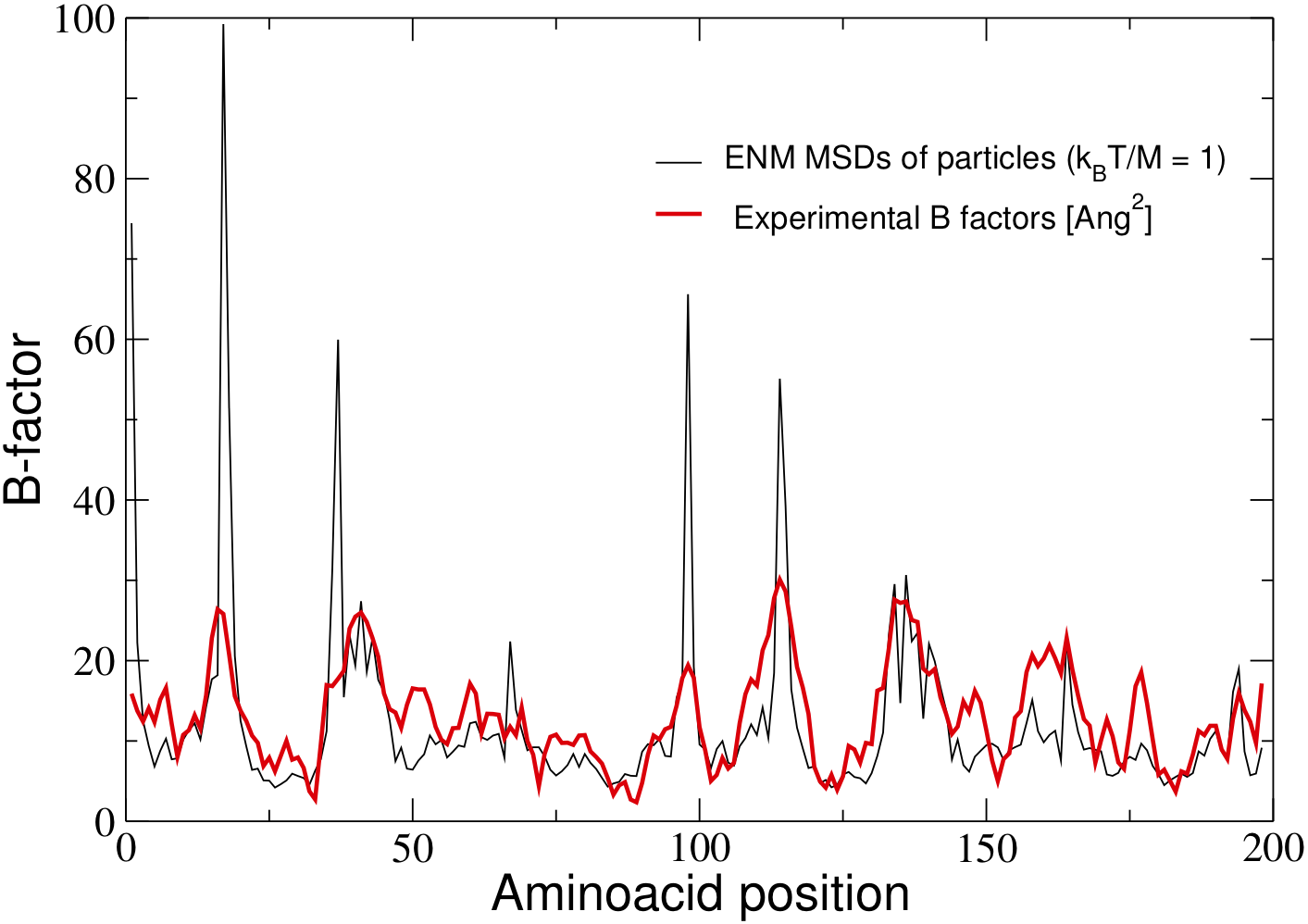
    Code
    Generic Fortran 90 code, two arguments: PDB file and cutoff [Ang]

    Data
    NM frequencies (cm^-1)
    Normalized displacement pattern of the highest-frequency NM
    Normalized displacement pattern of the lowest-frequency NM


Course on Introduction to numerical solution of partial differential equations: the diffusion equation
Academic year 2018/2019, university of Orleans

  • Python script to solve the 1D diffusion equation in the interval [0,L] with a simple explicit method. The example illustrates diffusion through a slab (e.g. the skin stratum corneum) kept at a fixed concentration at its leftmost side (e.g. the skin/air interface) and in contact with a sink at its rightmost side (e.g. diffusion into the epidermis).
  • Python script to solve the 1D diffusion equation in the interval [0,L] with the Crank-Nicholson method. The example illustrates the time evolution of a sinusoidal profile, constant Dirichlet boundary conditions at x=0 and x=L.
  • A short note describing the methods implemented above.

Some useful Gnuplot scripts

  • Gnuplot script to generate a postscript image of a 2D vector field. The components of the field are specified as functions of (x,y) and the arrows are color-coded according to the local strentgh of the field (i.e. the norm). The user can also choose to plot the direction field, i.e. the normalized vector field - same color coding but arrows of the same length at each point.
  • Gnuplot script Basic gnuplot script to generate a cool-looking encapsulated postscript figure for your reports.

Cours de physique statistique avancée, EPFL, a.a. 2004/2005




Corso di Fisica generale I, Università di Firenze, 2002-2003
Facoltà di Ingegneria dell'ambiente e delle risorse - PIN Prato (a.a. 2002/2003)