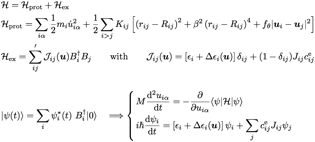Coarse-grained models

Nonlinear network models of protein dynamics

In order to investigate the structural and dynamical determinants of allosteric communication in proteins, we have introduced a modified version of the elastic-network scheme (Fig. 1), the Nonlinear Network Model (NNM) [Piazza2008, Piazza2009,Piazza2014]. More precisely, to study how mechanical perturbations are transmitted across protein structures, we have devised several original computational approaches, which were implemented in computer codes designed in-house. These include:

• Surface cooling [Juanico2007]. In these simulations, a thermalized system is subject to friction at its surface. During the cooling process, nonlinear effects cause spontaneous energy localization in the bulk of the system. This technique, applied in the framework of the NNM, has allowed us to isolate relevant hot spots in enzymes, i.e. amino acids at special positions which are close to the experimentally annotated active sites. This and related techniques proved very powerful in identifying hot spots and we are currently working at a computational model to predict active sites in enzymes [Aubailly2015].

• SMS-kick simulations [Piazza2009]. This approach has been devised to dissect important energy transduction pathways. A local kinetic energy kick is imparted at a given residue along the maximum stiffness direction. This is first determined by an original computational method that we have introduced, the Sequential Maximum Strain (SMS) protocol [Piazza2008]. The energy redistribution process is followed by computing (after a transient) the velocity covariance matrix, whose eigenvectors provide important clues on the energy redistribution process. We have devised a numerical approach to kick all sites and extract statistical indicators of energy conductivity (along specific bonds) and avidity (probability to transfer to a given site when energy is imparted elsewhere).

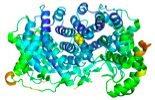
Figure 1. Coarse grained nonlinear network model (NNM). Each amino acid is replaced by an effective bead. Nonlinear springs are then stretched between pairs of particles that lie at a distance below a specified cutoff.

Coupled exciton-protein dynamics in light harvesting complexes

In the framework of our participation to the EU-FP7 project PAPETS (http://www.papets.eu/) we are developing an original computational model to describe the coupled dynamics of an exciton created at a given pigment in a light-harvesting complex and the dynamics of the embedding protein matrix. The total Hamiltonian is reported in Fig. 2. The protein is treated within the framework of a modified NNM, where angular interactions are also included. The exciton is described by a tight-binding Hamiltonian where site energies fluctuate, as they are coupled to the classical coordinates of the underlying protein system. The system is evolved in time by integrating numerically Schrödinger equation for the exciton and Newton’s equation for the protein. The goal is to investigate the role of specific, fold-encoded vibrational modes in the efficiency characterizing the transfer of one exciton from a pigment to a distant one. We are currently studying the LHCII antenna complex (higher plants, containing chlorophylls) and the PE545 antenna complex (Cryptomonads algae, containing bilins). We are also extending our computational approach to include fluctuations in the coupling terms in the exciton Hamiltonian, as these, while weaker than site energy fluctuations, can impact considerably on exciton transport [Vlaming2012].

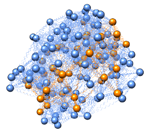
Figure 2. Left: Bead-and-springs coarse-grained representation of a light-harvesting trimer from LHCII (from spinach, structure provided by R. Croce, VUA, Amsterdam). Orange beads represent chlorophylls, light blue beads are aggregate amino acids in the protein matrix (shape-based CG [Freddolino2009]). Right: the semiclassical exciton-protein coupled model. The site energies in the tight-binding Hamiltonian for the exciton are modulated by the displacement field of the beads. Schrödinger equation for the exciton and Newton’s equation for the pigment+protein scaffold are evolved in time simultaneously.

All-atom molecular dynamics simulations

We are currently implementing a GPU-based all-atom molecular dynamics (MD) platform in our group running GROMACS 5.0. We have come to the conclusion that we need all-atom MD simulations as a complement to our activities for many reasons. Most importantly, topology-based CG models such as NNM, are insensitive to chemical details that may be important in the processes we are interested into. These include the formation/breaking of hydrogen bridges (within the protein and between the protein and water) and disulfide bonds (crucial for the large-scale stability of many proteins). Moreover, it is important to have an accurate description of the solvent available, especially for free energy calculations. The spirit with which we are doing this is two-fold. On the one hand, we wish to test our results obtained in the framework of more simplified schemes in more realistic environments. On the other hand, we are convinced that the development of simple, effective schemes has to be done bottom-up if possible, i.e. in such a way to conceive and parameterize coarse-grained models from first principles as much as possible.

Energy transfer and localization in proteins

We set out to repeat the surface cooling simulations performed with the NNM through all-atom MD simulations. This has entailed devising an original computational approach, where we simulate a protein in a box filled with water, which is progressively cooled down at a specified rate. 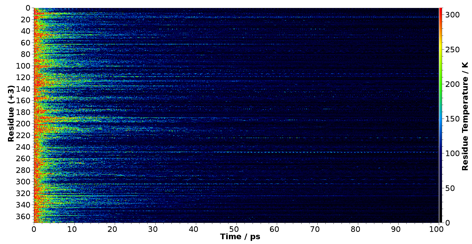In this way we avoid interacting explicitly with the protein and simulate as indirectly as possible the extraction of energy from its surface. Preliminary results (shown in Fig. 3) confirmed that energy self-localization in the bulk of the protein occurs also at the atomic level. We are currently in the process of characterizing this fascinating phenomenon and compare this with our NNM results. Localization of energy in proteins is thought since a long time to underlie many important processes, from photosynthesis to muscle contraction and enzyme catalysis [McClare1975].

Figure 3. Density map of local temperature versus time in an all-atom cooling simulation performed with Gromacs. The emergence of persistent, localized hot spots at specific sites out of the cooling process is evident.

Electron transfer and inelastic tunneling in olfactory receptors

Nobody knows which are the molecular bases of the sense of smell. Olfactory receptors are embedded in membranes separated from the nasal cavity by a mucus layer. Odorant molecules, diffuse (bound to carrier proteins) until they bind to a receptor. This triggers an allosteric response on the other side (inside the cell), which results in a protein (protein G) to bind to the receptor. This initiates a biochemical cascade, which eventually sends a stimulus to olfactory neurons. Nobody knows what causes a given odorant to be recognized by a receptor. The combinatorial aspects of the problem are very complex, many odorant being recognized by a given receptor and viceversa. To make things worse, no structure exists at present of an olfactory receptor.

In the framework of the PAPETS project, we are studying this fascinating problem from many points of view. On one side, we are collaborating with a group at the University of Nantes with strong expertise in sequence alignment and structure prediction. The goal of this collaboration is to produce a pattern of (i) highly conserved residues and (ii) co-evolving residues across the entire pool of olfactory receptor sequences (these are all known). Our goal is to set up a new computational strategy to connect this phylogenetic information with structural and dynamical correlations. We plan to obtain these through MD simulations of coarse-grained and all-atoms schemes in parallel. The rationale behind this project is that evolution has probably conserved residues, which are important at a structural and dynamical level for the molecular functions.

Olfactory receptors are a family (accounting for about half of the population) of the more general G-protein coupled receptors (GPCR). To give an idea of the importance of these receptors (whose job is to bind a ligand outside the cell and transmit a signal into the cell through the membrane), it is enough to realize that more than 60 % of current drug targets are GPCRs. Although the sequences are very different, all GPCRs share the same fold and the same overall mechanism of allosteric trigger. Therefore, we will compare our analysis of different models of the olfactory receptor OR1G1 with similar analyses of known structures of other GPCRSs, such as the beta-2 adrenergic receptor 2RH1. Moreover, we will compare coarse-grained and atomistic simulations in the effort of retrieving the important structural and dynamical correlations matching the patterns of conservation and co-evolution.

Specifically to the olfactory receptors, we will investigate the possibility that ligands are recognized (also) by their vibrational spectra, a theory put forward by Luca Turin in 1996 that hypothesizes that a tunneling electron current is triggered upon ligand binding [Turin1996]. For this we will compare the vibrational spectra computed through DFT of more than 100 known odorant molecules that bind to OR1G1 whose binding affinities are known from calcium imaging measurements [Bootman2011].

Reaction-diffusion dynamics with ultra-coarse-grained models of large, flexible biomolecules

Statistics of conformations reproduced by shape-based models

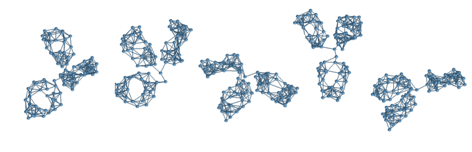
An important part of our group’s activities is the development of original computational strategies for the investigation of reaction-diffusion dynamics in complex systems. For example, we have a long-standing interest in the dynamics of formation of antigen-antibody complexes. Immunoglobulins G(IgG) are large and extremely flexible three-lobe molecules [Bongini2004]. In the cartoon right, I am depicting an ultra-coarse-grained model that we recently constructed with the purpose of investigating the role of the IgG conformation on its ability to bind a small antigen that is swiftly diffusing around. The model consists of 96 hard spheres joined by stiff springs. The result is a three-lobe structure where the three domains are free to move about the common hinging point at the centre of the molecule. The important point is that the three domains (two Fab arms, on whose tips lie the antigen-binding sites and the Fc stem below) keep their correct shape, imposed by the crystallographic structure (shown as a transparent surface in the cartoon) while fluctuating around each another. 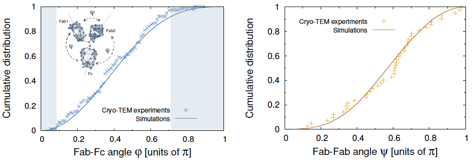Constant-energy MD simulations in vacuum of this model realized by means of a computer code realized in-house from scratch (a repulsive energy was also added to account for excluded-volume interactions among the three domains) shows that the experimental distributions of the inter-domain angles (measure by cryo-ET [Bongini2004]) are perfectly reproduced with no adjustable parameters (see Fig. 4). This is a remarkable result, as it shows that for large and flexible biomolecules it is key to consider excluded-volume interactions with account of the correct shape of the biomolecule(s).

Computing binding rate constants for different conformations

We developed an original mixed analytical/computational strategy to compute the binding rate constant of a small antigen to an antibody in a given conformation, sampled from an MD trajectory of our ultra-CG model. Our scheme is based on the stationary solution of the Laplace equation with a complex set of boundary conditions that account for the IgG conformation. These are a collection of reflective spherical boundaries (the spheres composing the IgG molecule in our CG representation) and two absorbing spherical boundaries (the two active sites, the paratopes, at the tips of the Fab arms). The solution of such complex boundary problem can be obtained formally in closed form by using known addition theorems of spherical harmonics [Morse1953]. The binding rate constant can be then computed to any desired accuracy by truncating an infinite-dimensional linear system.

Figure 4. Upper panel: a few configurations sampled from a constant-energy MD trajectory of our shape-based CG model of IgGs. Lower panels: comparison of the equilibrium distributions of inter-domain angles extracted from the simulations with the results of Cryo-ET experiments [Bongini2004].

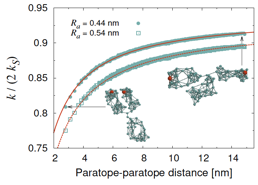
Small antigens see the IgG as an immobile obstacle with its realistic shape (the reflective spherical boundaries) and are adsorbed at the active sites (diffusion-limited binding, i.e. infinitely fast chemical fixation step once the encounter complex is formed). The results [Galanti2015] show that the whole binding process can be assimilated to that of two nearly isolated binding sites a fixed distance apart (dumbbell model). Surprisingly, the only effect of the large IgG body is to bring about a near-unity (0.94 to 0.96) constant reduction factor, independently of the configuration (see Fig. 5). In the next step of this project, we are planning to employ this original computational protocol to investigate the role of large-scale conformational motion on (i) proteins binding to DNA and (ii) small substrates binding to different enzymes (coarse-grained to the residue level).

Figure 5. Rate constant as a function of the distance between the active sites (red beads in the snapshots) for two different choices of the encounter distance Ra = paratope size + antigen size. The rate constant is normalized by twice the Smoluchowski rate constant of an isolated paratope. The solid lines are plots of the nearly isolated dumbbell-like model where fa < 1 is a reduction factor and d is the paratope-paratope distance.

References

[Aubailly2105] S. Aubailly and F. Piazza, Cutoff lensing: predicting catalytic sites in enzymes, to appear in Scientific Reports (2015).
[Bongini2004] L. Bongini, D. Fanelli, F. Piazza, P. De Los Rios, S. Sandin, and U. Skoglund, Proceedings of the National Academy of Sciences of the United States of America 101, 6466 (2004).
[Bootman2011] Bootman, M. D., & Roderick, H. L. (2011). Using calcium imaging as a readout of GPCR activation. Methods in Molecular Biology, 746, 277ø296.
[Freddolino 2009] Freddolino, P. L., Arkhipov, A., Shih, A. Y., Yin, Y., Chen, Z., & Schulten, K. (2009). Application of Residue-Based and Shape-Based Coarse Graining to Biomolecular Simulations. In Multiscale Simulation Methods in Molecular Sciences (Vol. 42, pp. 445ø 466).
[Galanti2015] M. Galanti, D. Fanelli and F. Piazza, (2015) The role of the antibody conformation in the formation of encounter complexes with small antigens, revised manuscript in preparation for Scientific Reports.
[Juanico2007] Juanico, B., Sanejouand, Y. H., Piazza, F., & De Los Rios, P. (2007). Discrete breathers in nonlinear network models of proteins. Physical Review Letters, 99. 238104.
[McClare1975] McClare, C. W. (1975). How does ATP act as an energy source? Ciba Foundation Symposium, 301ø325.
[Morse1953] P. M. Morse and H. Feshbach, Methods of theoretical physics, Vol. 2 (McGraw-Hill Science/Engineering/Math, 1953) pp. 409-415.
[Piazza2008] Piazza, F., & Sanejouand, Y.-H. (2008). Discrete breathers in protein structures. Physical Biology, 5(2), 026001.
[Piazza2009] Piazza, F., & Sanejouand, Y.-H. (2009). Long-range energy transfer in proteins. Physical Biology, 6(4), 046014.
[Piazza2014] Piazza, F. (2014). Nonlinear excitations match correlated motions unveiled by NMR in proteins: a new perspective on allosteric cross-talk. Physical Biology, 11, 036003.
[Turin1996] Turin, L. (1996). A spectroscopic mechanism for primary olfactory reception. Chemical Senses, 21, 773ø791.
[Vlaming2012] Vlaming, S. M., & Silbey, R. J. (2012). Correlated intermolecular coupling fluctuations in photosynthetic complexes. The Journal of Chemical Physics, 136(5), 055102.